Persamaan Posisi, Kecepatan, Percepatan, Pembuktian Rumus GLBB, dan Grafik
- Daffa Sadek
- 24 Des 2017
- 4 menit membaca
Kenapa sih ada rumus GLBB yang ada 3 itu? Bagaimana sih cara membaca grafik_grafik GLBB?. Sebelum lanjut membaca sebaiknya kalian tuntaskan rasa lapar, hilangkan beban pikiran, dan lupakan kenangan pahit tentang mantan yang bisa membuat kalian gagal fokus. Jika sudah, then read on...

Perjalanan dari rumah saya ke sekolah yang jaraknya 20 km memerlukan waktu 30 menit. Kecepatan saya kira-kira sekitar 40 km/jam. Tapi apakah saya terus menerus kecepatannya 40 km/jam? Saat menit-menit pertama dari rumah jalanan kosong sehingga bisa sampai 60 km/jam, tetapi saat mendekati sekolah bisa saja turun menjadi 20 km/jam. Nah lalu kecepatan sesaat saya berada di menit ke 14 berapa? Itu lah yang akan kita bahas pertama disini.
Diatas adalah contoh kasus seorang pelajar bernama "saya" bukan berarti itu penulis blog ini ya. Kalo saya enggak ngebut kok gak perlu dilapor.
Pertama-tama kita kan tahu bahwa rumus kecepatan adalah perubahan jarak terhadap waktu dan percepatan adalah perubahan kecepatan terhadap waktu. Perhatikan bahwa kecepatan adalah jarak dibagi waktu, dan percepatan adalah kecepatan dibagi waktu. Seakan-akan kayak turun gitu dibagi-bagi terus sama waktu. Dan memang kenyataannya itu.
Kecepatan adalah turunan jarak terhadap waktu dan percepatan adalah turunan kecepatan terhadap waktu.
Kebalikan dari turunan adalah naikkan. Beneran gak ngelawak beberapa orang panggilnya gitu. Nama yang lebih lazim adalah integral. Maka jarak adalah integral dari kecepatan dan kecepatan adalah integral dari percepatan. Kalau digambar biar keliatan lebih enaknya seperti ini:

Gambar diatas menunjukkan kalau kalian ingin mencari kecepatan bisa diturunkan dari jarak. Kalau ingin mencari percepatan bisa dengan menurunkan kecepatan. Kalau ingin mencari jarak bisa meng-integralkan kecepatan. Apasih integral dan turunan itu? Kita bahasnya dangkal-dangkal aja karena kalau ingin lebih kompleks bukan disini bahasnya wkwkwk.
Sederhananya, turunan bisa dirumuskan seperti ini:

dy/dx dan y’ hanyalah penulisan lain dari turunan. Inti dari turunan (nama lainnya diferensial) hanya “menurunkan pangkat” suatu fungsi. Contoh soalnya begini:

Mudah kan? Perhatikan kalau yang diturunkan gak ada variabel x, maka hasilnya 0 (dicontoh 69 dan 4b). Kalau integral sih agak lebih ribet. Jadi rumusnya gini:

C itu adalah konstanta biasa. Kalau di turunan, pangkatnya dikalikan dulu baru dikurang, di integral ditambah dulu baru dikalikan. Perhatikan saja contoh soalnya seperti ini:

Kalian sadar tidak contoh soal integral nomor 2 adalah jawaban dari soal turunan nomor 1? Di soal nomor 1, 69 akan hilang karena dia tidak memiliki x saat diturunkan. Nah di soal no 2, bagaimana kita bisa mencari angka 69? Gak bisa sama sekali. Makanya kita cuma tulis + C saja.
Ngerti? Bingung? Untuk contoh soalnya, tunggu saja postingan selanjutnya agar kalian jadi lebih mengerti yaa, nah sekarang kita akan mencari penurunan 3 rumus penting GLBB yang kalian harus pahami.
Penurunan Rumus-Rumus GLBB
Kenapa sih perlu ada penurunan rumus? Percayalah kalian perlu bisa menurunkan rumus sendiri. Selain kalian akan lebih mengerti rumus itu sehingga penerapannya lebih luas, kalian juga akan terbiasa dengan kuliah. Saran dari kakak-kakak alumni saya, jangan mudah terlena dengan rumus cepat begitu. Kita mulai dari yang pertama, yakni yang paling mudah. Perhatikan penurunan rumus berikut! Percepatan adalah perubahan kecepatan terhadap waktu, maka:

Lambangnya bisa + atau – tergantung dari bendanya, apakah dia mengalami percepatan atau perlambatan.
Yang kedua kalian perlu memahami integral dan turunan diatas. Jarak (S) adalah integral dari kecepatan, maka untuk mendapatkan rumus s kita perlu meng-integralkan dulu rumus kecepatan diatas.

S0 ini adalah jarak saat waktunya 0, atau jarak awal benda sebelum dia bergerak. Bisa saja benda itu sebelum bergerak udah berjarak 50m dari kita, nah itu akan menjadi faktor penentu jarak benda itu dari kita pada detik ke-t.
Untuk rumus ketiga, saya nyarinya sih agak panjang sedikit, tapi penurunan rumusnya seperti dibawah ini. Kita akan menganggap bahwa jarak awal benda itu adalah 0. Di rumus ketiga ini tidak ada t sama sekali. Gunakan rumus yang pertama untuk mendapatkan rumus t.

Grafik GLB dan GLBB
Belum pusing? Nah kita selanjutnya akan membahas grafik. Kalian harus bisa membaca grafik dan mengolah informasi yang didapat dari grafik. Dibawah ini adalah beberapa grafik yang menyatakan berbagai informasi tentang GLB

Grafik yang kiri dan tengah itu sumbu-sumbunya jarak dan waktu. Untuk menghitung kecepatan, cukup membagi jarak dengan waktu di suatu titik. Kalau garisnya naik gunung dari kiri ke kanan maka kecepatan dia kecepatannya positif, kalau garisnya turun lembah maka kecepatannya negatif. Bahasa matematikanya kecepatan adalah gradien dari grafik hubungan jarak-waktu.
Kalau di grafik hubungan kecepatan dan waktu (yang kanan), bentuknya pasti garis lurus karena kecepatan di GLB itu konstan. Maka untuk menghitung jarak dari grafik ini kalian cukup mengingat saja rumus jarak, yakni kecepatan kali waktu.
Nah dibawah ini adalah grafik tentang GLBB.
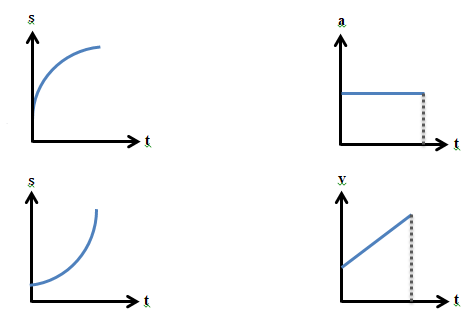
Diatas adalah grafik GLBB. Grafik dikiri atas yang bentuknya kayak setengah pelangi itu adalah grafik hubungan antara jarak dan waktu yang menunjukkan percepatan positif. Kalau bentuknya yang kayak perosotan menghadap ke kiri itu juga sama menunjukkan grafik antara jarak dan waktu, bedanya percepatannya negatif atau benda itu mengalami perlambatan.
Kalau dibawa ke bahasa matematika, rumus jarak itu kan seperti bentuk parabola. Jika kecepatan adalah turunan dari jarak terhadap waktu, maka di grafik itu kecepatan adalah garis singgung parabola tersebut! (buat yang gak ngerti: Jika kalian menurunkan rumus parabola, hasilnya adalah rumus garis singgung parabola tersebut)
Di grafik hubungan v-t, a adalah gradien dari garis miring itu. Jadi sederhananya sama kayak grafik hubungan s-t di GLB. a bisa dicari dengan membagi perbedaan kecepatan dengan waktu. Kalau s nya apa? yaa jaraknya secara gampang bisa dicari dengan mencari luas bangunan trapesium itu. Kalau bangunnya segitiga yaa luas segitiga yang dicari.
Kalau di grafik hubungan a-t, kalian dapat mencari v dengan menghitung luas persegi panjang grafiknya!
Apakah bentuk grafiknya pasti begitu? Enggak juga. Jika kita mengasumsikan persamaan panjangnya berbentuk persamaan kuadrat, maka iya grafiknya akan seperti itu. Tetapi jika sudah berbentuk polinom (pangkat banyak) yaa beda lagi tergantung pangkat berapa. Jangan lupa baca-baca lagi tentang bentuk-bentuk grafik untuk setiap pangkat yang berbeda. Untuk pengolahannya kurang lebih sama.




Komentar